Mathematical Treatment

From Section 1, we know that at each peak, $\alpha = m\pi$, and

$$\alpha=\frac{ka}{2}\sin \theta =\left(\frac{2\pi}{\lambda} \... ...\frac{a}{2}\sin \theta =\frac{\pi a}{\lambda}\sin \theta =m\pi$$

$$\frac{a}{\lambda}\sin \theta=m$$

$$\sin \theta = \frac{m\lambda}{a}$$

But for very small angles, $\sin \theta \approx \theta$, and here, $\lambda/a$ is of the magnitude of $1 \times 10^{-4}$, so

$$\theta \approx \frac{m\lambda}{a}$$ (5)

This means that if we want to compare the angle of diffraction for 2 slightly different wavelengths,

$$\Delta \theta \approx m\frac{\Delta \lambda}{a}$$ (6)

The separation between the peaks of the two wavelengths will therefore increase linearly with order number, with a slope of $\Delta \lambda /a$.

The TRACE specifications say that the grating has 70 lines per inch, so $a = 3.63 \times 10^{-4}$ m.

Using equation (6), we can calculate that the slope of the line should be

$$\frac{\Delta \lambda}{a} =\frac{1.7452 \times 10^{-8} - 1.7106 \times 10^{-8}} {3.63 \times 10^{-8}} =9.535 \times 10^{-7}$$

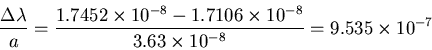
That is, the separation between the peaks of the two wavelengths will increase by $9.535 \times 10^{-7}$ radians (0.1967 arc sec) per order. The TRACE specifications say that each pixel is 0.4993 arc seconds across, so the separation between the peaks should increase by 0.1967/0.4993 = 0.394 pixels per order number.