 |
We can represent the wire mesh by a two-dimensional series of square slits. In each dimension, this can be represented as a series of slits, as shown in Fig. 4.
We consider the following parameters:
![]() = the angle that the light is diffracted by -- the angle between
the light ray and the line perpendicular to the mesh
= the angle that the light is diffracted by -- the angle between
the light ray and the line perpendicular to the mesh
![]() = the distance between slits
= the distance between slits
![]() = the width of each slit
= the width of each slit
![]() = the total number of slits
= the total number of slits
![]() = the wavelength of the light (171 Å)
= the wavelength of the light (171 Å)
![]()
![]() = the order number
= the order number
We define
![]() and
and
![]() .
.
The relevant specifications of the TRACE telescope front filter mesh are as follows: There are 70 lines per inch, i.e.
![]() m; the transmission of the mesh is 82%; and each pixel has a spatial span of 0.4993 arc seconds.
m; the transmission of the mesh is 82%; and each pixel has a spatial span of 0.4993 arc seconds.
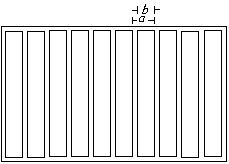
This equation describes the light density distribution after passing through a series of slits on a grating [Hecht and Zajac, Optics, 1974, p. 344]:
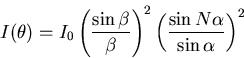 |
(1) |
At each principal maximum, ![]() , where
, where ![]() is the order number, i.e.,
is the order number, i.e., ![]() is a whole multiple of
is a whole multiple of ![]() . That means, in the term
. That means, in the term
![]() , both the numerator and denominator approach zero as
, both the numerator and denominator approach zero as ![]() approaches
approaches ![]() . Using L'Hopital's Rule, we have:
. Using L'Hopital's Rule, we have:
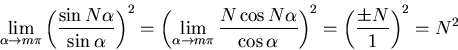
Thus,
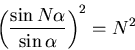 |
(2) |
at every principal maximum. Since we are concerned only with the pattern of the principal maxima, we can ignore
![]() because it is the same for each peak.
because it is the same for each peak.
![]() is the term which determines the pattern we see in the principal maxima.
is the term which determines the pattern we see in the principal maxima.
To find out what
![]() is at each peak, we must solve for
is at each peak, we must solve for ![]() in terms of
in terms of ![]() , the order number.
, the order number.
![]()
![]() (multiply both sides by
(multiply both sides by ![]() )
)
But
![]() is defined to be
is defined to be ![]() , so
, so
![]() .
.
Substituting for ![]() in equation (1), and using equation (2), we get:
in equation (1), and using equation (2), we get:
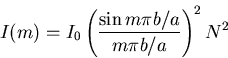 |
(3) |
At the zeroth order position,
![]() , and
, and
![]() (because
(because
![]() )
so dividing equation (3) by I(0),
)
so dividing equation (3) by I(0),
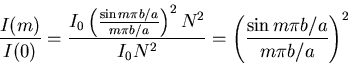
or
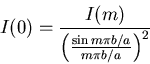 |
(4) |
This equation relates the zeroth order intensity with that of any of the other orders.
According to this theoretical description, the only number needed to apply Equation (4) is the value of ![]() .
.
A simple numerical calculation adding up orders from 1 to 23 shows that if light is diffracted in four directions as observed in the May 16 flare, 20.0% of the light is diffracted away from the zeroth order.