


Next: Results from March 15
Up: Extrapolating the Flare Intensity
Previous: Method
Table 1 shows the data. +45, etc. indicates the direction of the arm of the diffraction pattern; +45 indicates 45 degrees up from right, -45 indicates 45 degrees down from right, etc.
Table 1:
Intensities of each peak in the diffraction pattern: May 16, 1999
order# (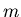 ) ) |
+45 |
+135 |
-135 |
-45 |
average |
st. dev. |
| 1 |
20578.4 |
20235 |
27072 |
25751.2 |
23409 |
3511 |
| 2 |
20779.8 |
18306 |
20992 |
- |
20026 |
1493 |
| 3 |
18612.2 |
17100 |
13721.6 |
13161.4 |
15649 |
2632 |
| 4 |
11919.6 |
11960 |
13790 |
11586.4 |
12314 |
998 |
| 5 |
6980.4 |
7954 |
6177.6 |
6901.2 |
7003 |
729 |
| 6 |
3697.4 |
3650 |
2705 |
3908.8 |
3490 |
535 |
| 7 |
1016.4 |
1352 |
1584 |
1028.5 |
1245 |
274 |
| 8 |
- |
171.5 |
- |
91.2 |
131 |
57 |
| 9 |
0 |
0 |
0 |
0 |
0 |
- |
| 10 |
345.6 |
399 |
262.5 |
324 |
333 |
57 |
| 11 |
699.6 |
907.2 |
815 |
489.6 |
728 |
180 |
| 12 |
985.8 |
1440 |
1170 |
980 |
1144 |
216 |
| 13 |
984 |
1505 |
1320 |
817.6 |
1157 |
312 |
| 14 |
608 |
837 |
745.2 |
562.5 |
688 |
125 |
| 15 |
- |
- |
800 |
365.7 |
583 |
307 |
| 16 |
- |
- |
0 |
0 |
0 |
- |
| 17 |
- |
- |
0 |
0 |
0 |
- |
| 18 |
- |
- |
0 |
0 |
0 |
- |
| 19 |
- |
- |
0 |
0 |
0 |
- |
| 20 |
- |
- |
253 |
255 |
254 |
1.4 |
| 21 |
- |
- |
279 |
245.7 |
262 |
34 |
| 22 |
- |
- |
204 |
202.1 |
203 |
2.3 |
| 23 |
- |
- |
369.6 |
- |
369.6 |
- |
The value of 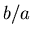 : Analyzing the data, we see that the intensity of the peaks drops to zero slightly before the 9th order (because the 8th order is much dimmer than the 10th order), and right between the 17th and 18th orders. So the intensity vanishes close to every 9 orders. We conclude that
: Analyzing the data, we see that the intensity of the peaks drops to zero slightly before the 9th order (because the 8th order is much dimmer than the 10th order), and right between the 17th and 18th orders. So the intensity vanishes close to every 9 orders. We conclude that 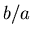 must be close to an even fraction of 9, such as
must be close to an even fraction of 9, such as 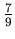 ,
, 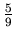 , etc. The transmission of the grating is 82%, and since
, etc. The transmission of the grating is 82%, and since 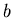 is the width of the opening and
is the width of the opening and 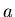 is the distance between openings,
is the distance between openings,
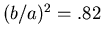 , or
, or
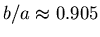 . The closest fraction of 9 to 0.9 is
. The closest fraction of 9 to 0.9 is 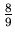 = 0.889. Since the graph actually dips slightly more often than every 9 orders,
= 0.889. Since the graph actually dips slightly more often than every 9 orders, 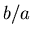 is probably slightly smaller than
is probably slightly smaller than 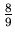 . The value that best fits the zeroes of the orders is 0.885.
. The value that best fits the zeroes of the orders is 0.885.
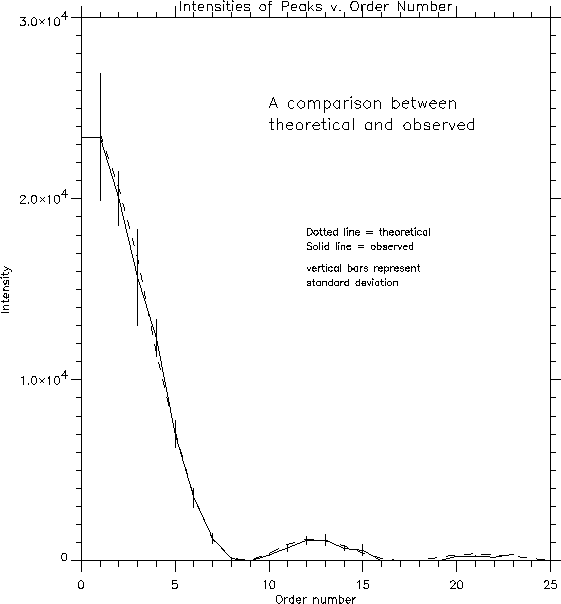
Fig. 5 shows that the theoretical curve fits the data very well. This would lead us to believe that we have used the correct theoretical representation of the diffraction pattern.
Figure 5:
The dotted line represents
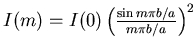 (where
(where 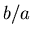 = 0.885)
= 0.885)
 |
Using Equation (4), we can take any order peak and plug the intensity in as 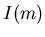 , and divide by the modulating function to find
, and divide by the modulating function to find 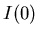 . We used the first seven orders to calculate an average extrapolated value for
. We used the first seven orders to calculate an average extrapolated value for 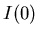 (see Table 2).
(see Table 2).
Table 2:
Predicted intensity of zeroth order
| order# |
Average 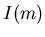 |
Predicted 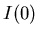 (by equation (4)) (by equation (4)) |
| 1 |
23409 |
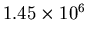 |
| 2 |
20026 |
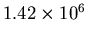 |
| 3 |
15649 |
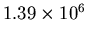 |
| 4 |
12314 |
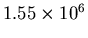 |
| 5 |
7003 |
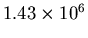 |
| 6 |
3490 |
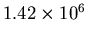 |
| 7 |
1245 |
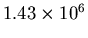 |
We obtain an average result of
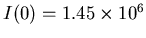 . The uncertainty of the mean is
. The uncertainty of the mean is
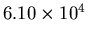 , about 4.2% of the calculated value.
, about 4.2% of the calculated value.
We must keep in mind that the zeroth order does not give the actual intensity of the flare, only the largest portion of it. Much of the light is diffracted off into the diffraction pattern, so to find the actual intensity of the flare, we have to add together all the orders. This gives us
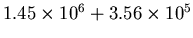 (we add the zeroth order to the total of the intensities of all the peaks; but since orders past
(we add the zeroth order to the total of the intensities of all the peaks; but since orders past 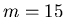 are cut off in the +45 and +135 arms, we take the average of each order and multiply by 4 to be the sum of the intensities in that order), which is
are cut off in the +45 and +135 arms, we take the average of each order and multiply by 4 to be the sum of the intensities in that order), which is
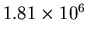 .
.
Significantly, the total intensity of the entire May 16 diffraction pattern through 23 orders is
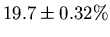 of the intensity of the flare. The error is derived from the standard deviations of each order. This means that 19.7% of all the light coming through the filter gets diffracted away from its original angle, even when the diffraction pattern is too dim to be visible. Also, this indicates that much of the light is being lost from the focused position and being spread out over the entire image. This is slightly less than the theoretical value of 20.0% diffracted away, but the theoretical value is within the inherent error of the number 19.7%.
of the intensity of the flare. The error is derived from the standard deviations of each order. This means that 19.7% of all the light coming through the filter gets diffracted away from its original angle, even when the diffraction pattern is too dim to be visible. Also, this indicates that much of the light is being lost from the focused position and being spread out over the entire image. This is slightly less than the theoretical value of 20.0% diffracted away, but the theoretical value is within the inherent error of the number 19.7%.
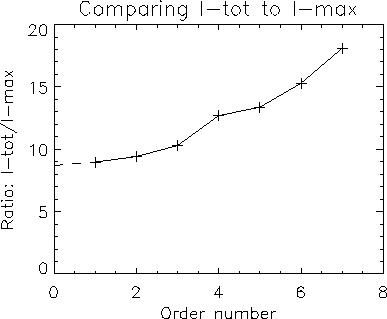
Now we examine how the intensity range of the camera has been increased. Table 3 compares the intensity of the highest pixel, 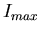 , to the total intensity,
, to the total intensity, 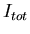 , at each order for the May 16th event.
, at each order for the May 16th event.
Table 3:
Comparing 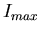 and
and 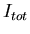 , at each order
, at each order
| order# |
Average 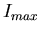 |
Average 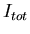 |
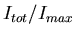 |
| 1 |
2610 |
23409 |
8.97 |
| 2 |
2127 |
20026 |
9.42 |
| 3 |
1515 |
15649 |
10.30 |
| 4 |
970 |
12314 |
12.70 |
| 5 |
524 |
7003 |
13.37 |
| 6 |
228 |
3490 |
15.30 |
| 7 |
69 |
1245 |
18.11 |
The graph in Fig. 6 shows that we can estimate that 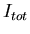 for the zeroth order to be 8.7 times greater than
for the zeroth order to be 8.7 times greater than 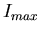 . We conclude that the highest pixel value is
. We conclude that the highest pixel value is
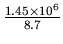 , or
, or
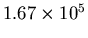 . This means that our intensity range has been effectively increased by a factor of 41, from 1 : 4096 to 1 :
. This means that our intensity range has been effectively increased by a factor of 41, from 1 : 4096 to 1 :
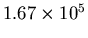 . Furthermore, we can expect that we can still use this method to determine intensities of even brighter flares; even if the diffraction pattern itself saturates, we can use higher orders to determine all of the orders, and the total intensity of the flare.
. Furthermore, we can expect that we can still use this method to determine intensities of even brighter flares; even if the diffraction pattern itself saturates, we can use higher orders to determine all of the orders, and the total intensity of the flare.
Figure 6:
The ratio
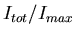 as a function of order number
as a function of order number  ;
we extrapolate backwards to find the ratio for the 0th order.
;
we extrapolate backwards to find the ratio for the 0th order.
 |



Next: Results from March 15
Up: Extrapolating the Flare Intensity
Previous: Method
Andrew Lin
2000-06-30
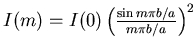 (where
(where 
